Evaluating a predictive model#
This notebook will:
Introduce linear models for regression tasks
Demonstrate scikit-learn’s user API
Explain training and testing error concepts
Cover cross-validation techniques
Compare models against baselines
Linear regression introduction#
Let’s start with linear regression fundamentals. We’ll use only NumPy initially, before introducing scikit-learn. First, we load our dataset.
# When using JupyterLite, you will need to uncomment and install the `skrub` package.
%pip install skrub
import matplotlib.pyplot as plt
import skrub
skrub.patch_display() # make nice display for pandas tables
/home/runner/work/traces-sklearn/traces-sklearn/.pixi/envs/docs/bin/python: No module named pip
Note: you may need to restart the kernel to use updated packages.
import pandas as pd
data = pd.read_csv("../datasets/penguins_regression.csv")
data
Processing column 1 / 2
Processing column 2 / 2
| Flipper Length (mm) | Body Mass (g) | |
|---|---|---|
| 0 | 181.0 | 3750.0 |
| 1 | 186.0 | 3800.0 |
| 2 | 195.0 | 3250.0 |
| 3 | 193.0 | 3450.0 |
| 4 | 190.0 | 3650.0 |
| 337 | 207.0 | 4000.0 |
| 338 | 202.0 | 3400.0 |
| 339 | 193.0 | 3775.0 |
| 340 | 210.0 | 4100.0 |
| 341 | 198.0 | 3775.0 |
Flipper Length (mm)
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 55 (16.1%)
- Mean ± Std
- 201. ± 14.1
- Median ± IQR
- 197. ± 23.0
- Min | Max
- 172. | 231.
Body Mass (g)
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 94 (27.5%)
- Mean ± Std
- 4.20e+03 ± 802.
- Median ± IQR
- 4.05e+03 ± 1.20e+03
- Min | Max
- 2.70e+03 | 6.30e+03
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
| Column | Column name | dtype | Null values | Unique values | Mean | Std | Min | Median | Max |
|---|---|---|---|---|---|---|---|---|---|
| 0 | Flipper Length (mm) | Float64DType | 0 (0.0%) | 55 (16.1%) | 201. | 14.1 | 172. | 197. | 231. |
| 1 | Body Mass (g) | Float64DType | 0 (0.0%) | 94 (27.5%) | 4.20e+03 | 802. | 2.70e+03 | 4.05e+03 | 6.30e+03 |
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
Flipper Length (mm)
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 55 (16.1%)
- Mean ± Std
- 201. ± 14.1
- Median ± IQR
- 197. ± 23.0
- Min | Max
- 172. | 231.
Body Mass (g)
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 94 (27.5%)
- Mean ± Std
- 4.20e+03 ± 802.
- Median ± IQR
- 4.05e+03 ± 1.20e+03
- Min | Max
- 2.70e+03 | 6.30e+03
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
| Column 1 | Column 2 | Cramér's V |
|---|---|---|
| Flipper Length (mm) | Body Mass (g) | 0.421 |
Please enable javascript
The skrub table reports need javascript to display correctly. If you are displaying a report in a Jupyter notebook and you see this message, you may need to re-execute the cell or to trust the notebook (button on the top right or "File > Trust notebook").
Our dataset contains penguin flipper lengths and body masses. We want to predict a penguin’s body mass from its flipper length. Since we predict a continuous value, this is a regression problem.
Let’s visualize the relationship between these measurements:
from matplotlib import pyplot as plt
ax = data.plot.scatter(x=data.columns[0], y=data.columns[1])
ax.set_title("Can I predict penguins' body mass?")
plt.show()
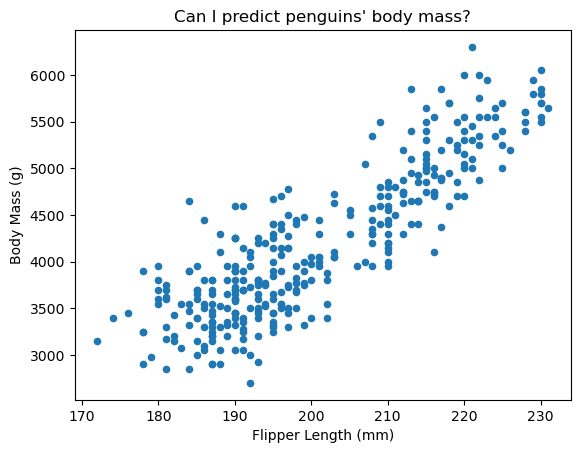
The data shows a clear linear trend - longer flippers correlate with heavier penguins. We’ll model this relationship linearly.
In this example:
Flipper length serves as our feature (predictor variable)
Body mass is our target (variable to predict)
Each (flipper length, body mass) pair forms a sample. We train our model on these feature/target pairs. At prediction time, we use only features to predict potential targets. To evaluate our model, we compare its predictions against known targets.
Throughout this notebook, we use:
X: feature matrix with shape(n_samples, n_features)y: target vector with shape(n_samples,)
X, y = data[["Flipper Length (mm)"]], data[["Body Mass (g)"]]
We model the X-y relationship linearly as:
where \(\beta\) represents our model coefficients. For all features, this expands to:
Here we have only one feature coefficient \(\beta_1\) for flipper length.
Finding the optimal \(\beta\) means finding values that minimize prediction error. We calculate \(\beta\) using:
which gives us:
EXERCISE
Use NumPy to find \(\beta\) (\(\beta_0\) and \(\beta_1\)) using the normal equation
Calculate predictions using your \(\beta\) values and X
Plot the original data (X vs y) and overlay your model’s predictions
# Write your code here.
Scikit-learn API introduction#
Scikit-learn uses Python classes to maintain model state. These classes provide:
A
fitmethod to learn parametersA
predictmethod to generate predictions
EXERCISE
Create a Python class that implements the linear model from above with:
A
fitmethod to compute \(\beta\)A
predictmethod that outputs predictions for input X
# Write your code here.
Now let’s use scikit-learn’s built-in LinearRegression model instead of our
implementation.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
Scikit-learn models store fitted parameters as attributes ending in underscore.
Our linear model stores coef_ and intercept_:
model.coef_, model.intercept_
(array([[49.68556641]]), array([-5780.83135808]))
Cross-validation for proper model evaluation#
Let’s evaluate our model’s performance:
from sklearn.metrics import r2_score
score = r2_score(y, model.predict(X))
print(f"Model score: {score:.2f}")
Model score: 0.76
This evaluation has a flaw. A model that simply memorizes training data would score perfectly. We need separate training and testing datasets to truly assess how well our model generalizes to new data. The training error measures model fit, while testing error measures generalization ability.
Let’s split our data into training and testing sets:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
model.fit(X_train, y_train)
model.coef_, model.intercept_
(array([[49.5057081]]), array([-5741.26490436]))
train_score = r2_score(y_train, model.predict(X_train))
print(f"Training score: {train_score:.2f}")
Training score: 0.75
test_score = r2_score(y_test, model.predict(X_test))
print(f"Testing score: {test_score:.2f}")
Testing score: 0.78
Our model performs slightly worse on test data than training data. For comparison, let’s examine a decision tree model which can show more dramatic differences:
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor(random_state=42)
model.fit(X_train, y_train)
DecisionTreeRegressor(random_state=42)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
DecisionTreeRegressor(random_state=42)
train_score = r2_score(y_train, model.predict(X_train))
print(f"Training score: {train_score:.2f}")
Training score: 0.83
test_score = r2_score(y_test, model.predict(X_test))
print(f"Testing score: {test_score:.2f}")
Testing score: 0.68
Returning to our linear model: while we see small differences between training and testing scores, we can’t determine if these differences are significant or just random variation from our data split. Cross-validation helps us estimate score distributions rather than single points.
Cross-validation repeatedly evaluates the model using different train/test splits to account for variation in both fitting and prediction.
model = LinearRegression()
Scikit-learn’s cross_validate function handles this repeated evaluation:
from sklearn.model_selection import KFold, cross_validate
cv = KFold(n_splits=5, shuffle=True, random_state=42)
cv_results = cross_validate(
model,
X,
y,
cv=cv,
scoring="r2",
return_train_score=True,
)
cv_results = pd.DataFrame(cv_results)
cv_results[["train_score", "test_score"]]
Processing column 1 / 2
Processing column 2 / 2
| train_score | test_score | |
|---|---|---|
| 0 | 0.755385535827193 | 0.7752714379193588 |
| 1 | 0.7669906545318712 | 0.7252369653654953 |
| 2 | 0.7636489994460085 | 0.741381163185274 |
| 3 | 0.7516847911210123 | 0.7837605603207971 |
| 4 | 0.7577138760016208 | 0.7597295576099133 |
train_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 5 (100.0%)
- Mean ± Std
- 0.759 ± 0.00620
- Median ± IQR
- 0.758 ± 0.00826
- Min | Max
- 0.752 | 0.767
test_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 5 (100.0%)
- Mean ± Std
- 0.757 ± 0.0240
- Median ± IQR
- 0.760 ± 0.0339
- Min | Max
- 0.725 | 0.784
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
| Column | Column name | dtype | Null values | Unique values | Mean | Std | Min | Median | Max |
|---|---|---|---|---|---|---|---|---|---|
| 0 | train_score | Float64DType | 0 (0.0%) | 5 (100.0%) | 0.759 | 0.00620 | 0.752 | 0.758 | 0.767 |
| 1 | test_score | Float64DType | 0 (0.0%) | 5 (100.0%) | 0.757 | 0.0240 | 0.725 | 0.760 | 0.784 |
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
train_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 5 (100.0%)
- Mean ± Std
- 0.759 ± 0.00620
- Median ± IQR
- 0.758 ± 0.00826
- Min | Max
- 0.752 | 0.767
test_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 5 (100.0%)
- Mean ± Std
- 0.757 ± 0.0240
- Median ± IQR
- 0.760 ± 0.0339
- Min | Max
- 0.725 | 0.784
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
| Column 1 | Column 2 | Cramér's V |
|---|---|---|
| train_score | test_score | 1.00 |
Please enable javascript
The skrub table reports need javascript to display correctly. If you are displaying a report in a Jupyter notebook and you see this message, you may need to re-execute the cell or to trust the notebook (button on the top right or "File > Trust notebook").
cv_results[["train_score", "test_score"]].mean()
train_score 0.759085
test_score 0.757076
dtype: float64
cv_results[["train_score", "test_score"]].std()
train_score 0.006198
test_score 0.024032
dtype: float64
Our results show similar train and test scores, though test scores vary more. Let’s use repeated k-fold cross-validation to get more estimates and visualize the score distributions:
from sklearn.model_selection import RepeatedKFold
cv = RepeatedKFold(n_repeats=10, n_splits=3, random_state=42)
cv_results = cross_validate(model, X, y, cv=cv, scoring="r2", return_train_score=True)
cv_results = pd.DataFrame(cv_results)
cv_results[["train_score", "test_score"]]
Processing column 1 / 2
Processing column 2 / 2
| train_score | test_score | |
|---|---|---|
| 0 | 0.7480477557099356 | 0.7809111483301286 |
| 1 | 0.7746497136935125 | 0.7317366217655594 |
| 2 | 0.7557198145912862 | 0.7650101620426033 |
| 3 | 0.7652740394451306 | 0.7448540824150485 |
| 4 | 0.7582280077453276 | 0.7512920310198041 |
| 25 | 0.7583449592589061 | 0.7602740475586415 |
| 26 | 0.7666072531133257 | 0.7232057649634724 |
| 27 | 0.7480829078085245 | 0.7806272407455322 |
| 28 | 0.7498103092540084 | 0.7687411379859436 |
| 29 | 0.7814185361409647 | 0.7049868668415336 |
train_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 30 (100.0%)
- Mean ± Std
- 0.759 ± 0.0159
- Median ± IQR
- 0.756 ± 0.0254
- Min | Max
- 0.727 | 0.785
test_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 30 (100.0%)
- Mean ± Std
- 0.750 ± 0.0341
- Median ± IQR
- 0.760 ± 0.0514
- Min | Max
- 0.675 | 0.809
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
| Column | Column name | dtype | Null values | Unique values | Mean | Std | Min | Median | Max |
|---|---|---|---|---|---|---|---|---|---|
| 0 | train_score | Float64DType | 0 (0.0%) | 30 (100.0%) | 0.759 | 0.0159 | 0.727 | 0.756 | 0.785 |
| 1 | test_score | Float64DType | 0 (0.0%) | 30 (100.0%) | 0.750 | 0.0341 | 0.675 | 0.760 | 0.809 |
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
train_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 30 (100.0%)
- Mean ± Std
- 0.759 ± 0.0159
- Median ± IQR
- 0.756 ± 0.0254
- Min | Max
- 0.727 | 0.785
test_score
Float64DType- Null values
- 0 (0.0%)
- Unique values
- 30 (100.0%)
- Mean ± Std
- 0.750 ± 0.0341
- Median ± IQR
- 0.760 ± 0.0514
- Min | Max
- 0.675 | 0.809
No columns match the selected filter: . You can change the column filter in the dropdown menu above.
| Column 1 | Column 2 | Cramér's V |
|---|---|---|
| train_score | test_score | 0.800 |
Please enable javascript
The skrub table reports need javascript to display correctly. If you are displaying a report in a Jupyter notebook and you see this message, you may need to re-execute the cell or to trust the notebook (button on the top right or "File > Trust notebook").
ax = cv_results[["train_score", "test_score"]].plot.hist(alpha=0.7)
ax.set(xlim=(0, 1), title="Distribution of the scores with repeated k-fold")
plt.show()
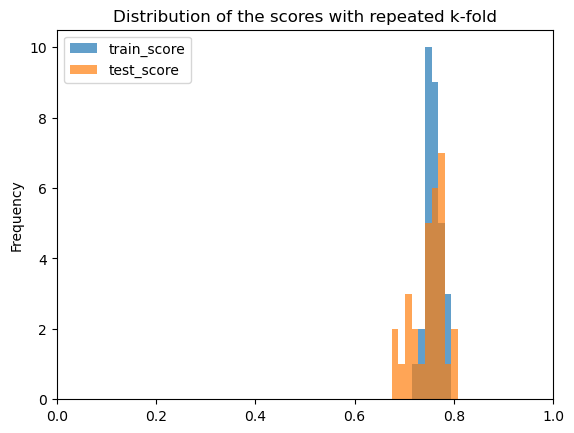
The similar performance on training and testing sets with low variation indicates our model generalizes well.
EXERCISE
Repeat the cross-validation using KFold with shuffle=False. Compare and explain
the differences from our previous analysis.
# Write your code here.
Baseline model comparison#
It is common to compare the performance of a new model against simple models. These baseline models do not necessarily have to learn anything from the data. But they provide a reference to compare against.
EXERCISE
Compare your linear model against such a baseline:
Use cross-validation to get 30+ score estimates
Try a
DummyRegressorthat predicts the mean target value of the training setUse
permutation_test_scorefunction to estimate the performance of a random modelPlot test score distributions for all three models
# Write your code here.
Model uncertainty evaluation#
Cross-validation evaluates uncertainty in the full fit/predict process by training different models on each cross-validation split.
For a single model, we can evaluate prediction uncertainty through bootstrapping:
model = LinearRegression()
model.fit(X_train, y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
EXERCISE
Generate model predictions on the test set
Create 100 bootstrap prediction samples using
np.random.choicePlot the bootstrap sample distribution
# Write your code here.